质疑_这是小升初考试题吗_怎么像极了中学几何题？

小学数学中常常会出现一些貌似属于中学知识范围的题型，乍一看，它们像极了中学数学题，且可用条件和线索隐蔽到似乎天衣无缝，难以挖掘利用。这种题往往会误导解题者们，使之思维方向与正确的解题路径南辕北辙，渐行渐远。究其缘由不外乎基础知识不扎实或方法运用生疏，造成思路闭塞和心理茫然，因而多学、多思、多练显得尤为重要，虽然这已是老生常谈，但其意义永存。

今天，笔者就选取一道这种唬人的“冒牌”题，用小学数学知识做一次精细的分析和解读，以飨读者。

看题——重点小学小升初真题：

如下图所示，三角形ABC的面积是36平方厘米，点D为AB边上的中点，FC与DE互相平行，那么三角形BEF的面积是多少平方厘米？

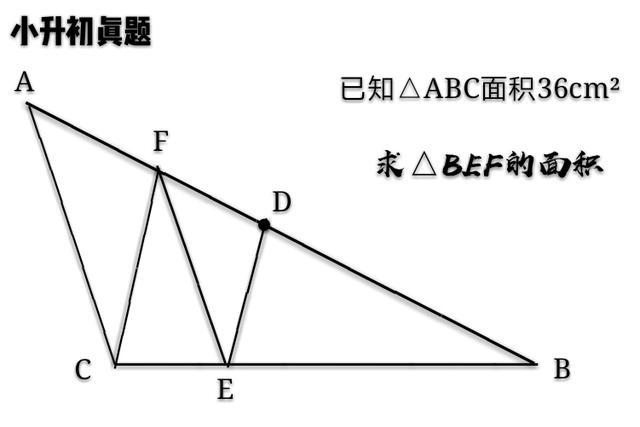
是不是像极了中学几何题？而它确确实实是小学题，甚至可以说是小学低年级数学题。首先，要充分利用已知条件进行综合考量，拨开障眼的迷雾，精准选取分析思考的起点。

根据已知条件，我们马上会联想到与解题相关的一些知识点：

（1）两条平行线间的距离处处相等；（2）等底等高的三角形面积相等；（3）中点的概念。

有了上述这些基础知识做后盾，再加上神奇的辅助线构图，即可轻轻松松秒解此题。

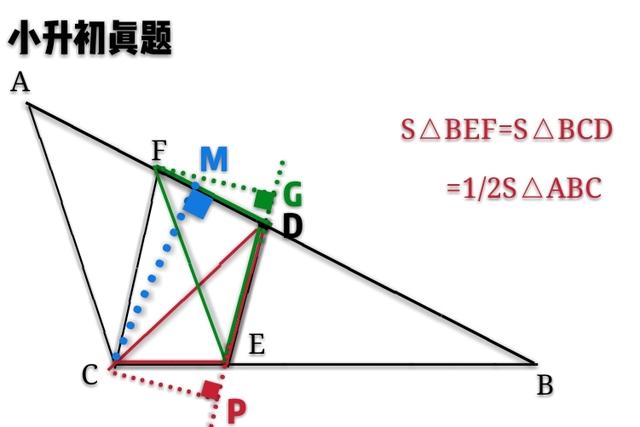
只需用一条辅助线连接CD，便能困惑顿消，思路豁然。为了便于理解，笔者分别用不同颜色的线段和虚线将图形重新构建了一下。

观察图形，红色三角形CDE和绿色三角形FED同底，它们的底都是线段DE。又因为FC与DE平行，所以CP=FG（两条平行线间的距离处处相等），而CP和FG分别是这两个三角形的高，等底等高面积相等。

S△CDE=S△FED。

把这两个三角形分别与三角形BDE组合，可得：

S△BDC=S△BEF。

接着，立刻将思考路径转入对“点D为AB边上的中点”这一条件的分析上来，可以轻而易举地得出：AD=BD。而AD和BD又分别为三角形ACD和三角形BCD的底，线段CM为这两个三角形共同的高，等底等高面积相等。因此三角形BCD的面积可求。

S△BCD=S△ACD=S△ABC÷2

=36÷2

=18（平方厘米）。

根据前面所证结论，亦可知三角形BEF的面积。

S△BEF=18（平方厘米）。

综上所述，从这道小升初几何题的解题过程，完全可以看出一个解题者的思维发散程度是否达标。要知道，根据已知条件，通过合理的想象构建一条直达问题核心的线索，这是一种最基本的不可或缺的思维能力，但这种能力的前提是要具有敏锐而活跃的思维触角，以及最大范围和最大限度的触角延伸。否则的话，困惑和蒙圈在所难免。